ТРАЕКТОРИЯ БРОШЕННОГО ТЕЛА

На любое брошенное тело действует сила притяжения Земли. В любой точке его траектории горизонтальная составляющая ускорения равна нулю, а вертикальная составляющая ускорения равна g, силе гравитационного поля (силе тяжести) в этой точке.

Вертикальное движение брошенного тела не зависит от горизонтального движения. Траекторию брошенного тела можно рассчитать с помощью уравнений динамики для движения с постоянным ускорением.

Если тело просто отпустили и оно падает вниз, не перемещаясь по горизонтали, то его скорость увеличивается равномерно с ускорением, равным g (ускорение свободного падения). Таким образом, через промежуток времени t после отпускания тела:

• его скорость v = gt;

• его средняя скорость будет равна gt/2;

• высота h уменьшится на величину, равную произведению средней скорости на время, и будет определяться по формуле gt2 /2.

Если тело бросили в горизонтальном направлении со скоростью V, то через промежуток времени t после броска:

• расстояние по горизонтали от точки броска x = Vt, так как его скорость постоянна;

• его вертикальное движение точно такое же, как и движение вертикально падающего тела, поэтому высота уменьшится на величину h = gt²/2.

Таким образом, траектория брошенного тела представляет собой кривую, которая по мере приближения к земле становится все круче и круче. Кривая такого типа называется параболой.

Траектория брошенного тела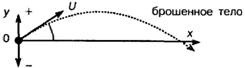

Если тело бросили под углом к горизонту, то в горизонтальном направлении оно проходит равные участки через равные промежутки времени. Скорость его вертикального движения уменьшается до нуля, а затем оно начинает падать с увеличивающейся скоростью. Его траектория представляет собой параболу, симметричную относительно своей наивысшей точки.

См. также статью «Динамика».