ВЕКТОРЫ

Векторной величиной называется любая физическая величина, имеющая наряду с числовым значением и направление. Перемещение, скорость, ускорение, сила, импульс, напряженность поля — все это векторные величины.

Скалярной величиной называется физическая величина, не имеющая направления. В качестве примеров можно привести расстояние, массу, энергию и мощность.

Векторную величину можно представить в виде направленного отрезка, длина которого пропорциональна числовому значению (модулю) величины, а направление совпадает с направлением величины. Вектор величины F, направленный под углом θ к некоей прямой линии, имеет две составляющие: F cos θ параллельно линии и F sin θ перпендикулярно линии. Если указанная линия является осью x системы координат, то Fx = F cos θ и Fy = F sin θ. Вектор можно разложить на составляющие i и j, направленные вдоль оси x и оси у соответственно, причем F = (F cos θ)i + (F sin θ)j.

Величину вектора F и его направление можно вычислить исходя из его перпендикулярных компонентов Fx и Fy по формуле

F = (F_x² + F_y²)^1/2 и tg θ = F_y/F_x, где θ — угол между вектором и осью х.

Сложение векторов

Правило параллелограмма для сложения векторов — точный геометрический метод нахождения результирующего вектора двух заданных векторов. Два вектора изображаются так, чтобы они образовывали две смежные стороны параллелограмма. Результирующим вектором будет его диагональ, направленная от начала первого вектора к концу второго. Два вектора прикладываются друг к другу так, чтобы конец первого был в той же точке, что и начало второго, поэтому сумма векторов — вектор, направленный из начала первого в конец второго.

Правило параллелограмма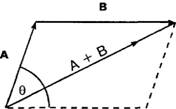

Правило косинусов для сложения двух векторов А и В предлагает следующую формулу для определения величины R результирующего вектора:

R² = А² + В² + 2АВ cos θ, где θ — угол между двумя векторами.

См. также статьи «Равновесие сил», «Сила и движение».